SisReN: Primeiros Passos: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 118: | Linha 118: | ||
*A variável com o maior t (t student) é a variável mais importante no modelo de regressão linear | *A variável com o maior t (t student) é a variável mais importante no modelo de regressão linear | ||
<br> | |||
{|style="border: 1px solid #9C9C9C" | {|style="border: 1px solid #9C9C9C" | ||
|- | |- | ||
Grau de Precisão||amplitude I.C. (80%) | |Grau de Precisão||amplitude I.C. (80%) | ||
|- | |- | ||
|III||≤ 30% | |III||≤ 30% | ||
Edição das 22h25min de 19 de agosto de 2014
ROTEIRO ANALISE MODELO REGRESSÃO
1. CRIA NOVO MODELO DE REGRESSÃO
- a partir da tela de Boas Vindas
- Ou a partir da barra de ferramentas padrão:
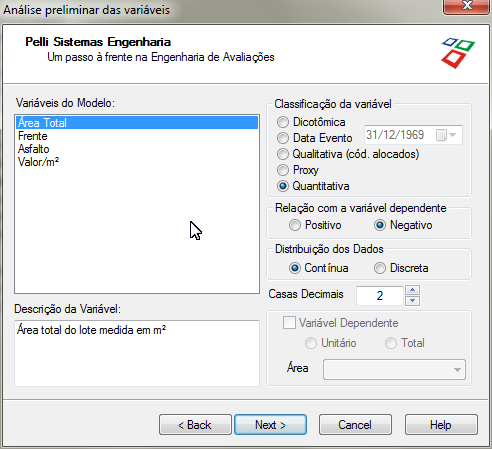
2. INFORMANDO DADOS PRELIMINARES DO MODELO
3. RETORNANDO AO MENU MODELO / PROPRIEDADES
- Variável dependente:
- Unitário (preferencialmente) OU
- Total
- Variáveis Independentes (ordem preferencial de construção das escalas)
- Quantitativas
- Dicotômicas
- Proxy e
- Qualitativas ordinais(Códigos Alocados)
Obs.: Códigos alocados, dicotômicas e quantitativas que podem ser contadas são variáveis discretas.
4. DIGITAÇÃO DOS DADOS DA AMOSTRA E DO IMÓVEL AVALIANDO
5. ANALISE EXPLORATÓRIA DOS DADOS DA AMOSTRA
- Estatística descritiva
- Gráficos de dispersão (Exibir Variáveis)
- Histogramas das Variáveis
- Medidas de tendência central, limites e dispersão
- No módulo exibir variáveis será possível:
- Identificar erros de digitação
- Extrapolação das variáveis independentes em relação aos imóveis avaliando;
- Identificar no gráfico os pontos discrepantes para cada variável independente;
- Tendência linear entre as variáveis independentes e variável dependente.
Por exemplo: Se a variável setor urbano aumenta, a localização do imóvel melhora e o valor deste deve aumentar. Se existir inversão, o problema pode ser de colinearidade ou existência de pontos influenciantes..
6. CALCULO DA EQUAÇÃO DE REGRESSÃO
![]()
- 6.1 – METODOS DE CÁLCULO
- GERAL – todas as regressões possíveis (combinação de todas as variáveis com todas as transformações selecionadas).
- SIMPLIFICADO – mais do que 10 variáveis e todas as transformações selecionadas (útil quando o cálculo da equação de regressão levar a um número muito grande de modelos e o tempo de espera pela resposta do programa também é grande);
- DIRIGIDO – reprodução de um modelo específico.
Iniciar com as transformações mais simples, isto é, x, 1/x e ln x
OBS.: as variáveis de códigos alocados podem ser transformadas(revisão realizada pela NBR 14.653-2, de 2011).
A estatística de DURBIN WATSON é específica para uso em séries temporais. Não deve ser utilizada com dados de corte transversal e nem com agrupamento de dados de corte transversal pois os resultados são inconsistentes. A sua utilização foi revista pela NBR 14.653-2 e não se aplica a dados de corte transversal.
Seleção do modelo deve ser preferencialmente pela estimativa.
Calculo Dos Coeficientes
- Deve-se utilizar o método dos mínimos quadrados para pequenas amostras; O método da máxima verossimalhança é utilizado para grandes amostras (>> 60).
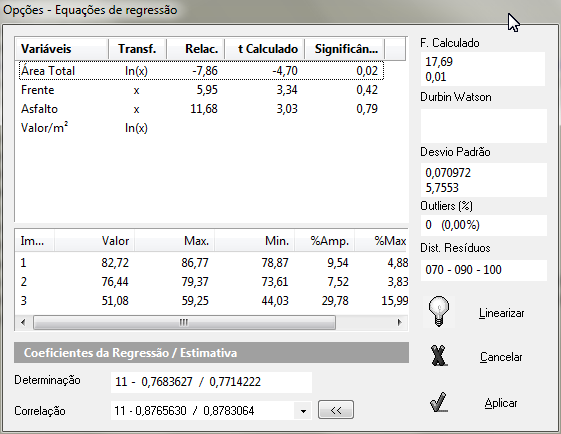
7. SELEÇÃO DO MODELO
- COEFICIENTE DE CORRELAÇÃO – desejável que seja maior que ou igual a 0,75 - indica uma correlação de média a forte entre as variáveis independentes e a variável dependente. Se o coeficiente é menor de 0,75, verificar e analisar se o modelo está corretamente especificado.
- TESTES FORMAIS – são aqueles cujos parâmetros de aceitação e rejeição são perfeitamente definidos na NBR 14.653-2.
| Significância do modelo (f) | Grau de Fundamentação |
| ≤ 1% | III |
| ≤ 2% | II |
| ≤ 5% | I |
| Significância das variáveis | Nível de confiança | Grau de Fundamentação |
| ≤ 10% | 90% | III |
| ≤ 20 % | 80% | II |
| ≤ 30 % | 70% | I |
- A variável com o maior t (t student) é a variável mais importante no modelo de regressão linear
| Grau de Precisão | amplitude I.C. (80%) |
| III | ≤ 30% |
| II | ≤ 40 % |
| I | ≤ 50 % |
- Obs.:
- O grau de precisão e de fundamentação não é afetado pelo uso de variáveis de códigos alocados.
- Verificar o sentido de variação da variável independente em relação à variável dependente:
- se é negativo ou positivo. Exemplo: a área aumenta o valor/m² deve diminuir.
DISTRIBUIÇÃO DOS RESIDUOS
[ 68 , 90 , 95 ] => Sugestão [ 66 a 74, 85 a 95, 95 a 100]
8. ANALISE DA EQUAÇÃO – verificar o gráfico da função estimativa.
- Inversão de variável independente irá aparecer em vermelho e os prováveis motivos são:
- pontos influenciantes,
- colinearidade ou
- falta de variável chave no modelo
O gráfico da projeção de valores para cada variável independente é ideal para análise de variáveis qualitativas, quantitativas e Proxy.
Para as variáveis DICOTOMICAS verificar a coluna da relação com a variável dependente. Exemplo dos lotes de Juiz de Fora, a inserção em condomínio, verifica-se que 21,39% de valorização para os que estão dentro do condomínio. Se desse abaixo de 15 % poderia arbitrar valores na necessidade de utilizar o “campo de arbítrio”.
Outro exemplo é o índice de aproveitamento. Para os imóveis com coeficiente de 1,8 o valor do imóvel será 44,07% , pois o poder construtivo do lote será bem maior do que daqueles com índice de aproveitamento de 1,.3
9. ANALISE DOS RESIDUOS
9.1 Resíduos da regressão
- HOMOCEDÁSTICO (erro constante),
- RESIDUO RELATIVO (coluna) - o ideal < 40 %
- RESIDUO RELATIVO (coluna) - > 70 % = TESTAR O MODELO S/O DADO
10. ADERENCIA
- Laudo na modalidade completo ou simplificado anexar o GRÁFICO ADERÊNCIA (valor estimado x preço observado).
- Pontos mais distantes da DIAGONAL (linha amarela) são os dados mais discrepantes, e devemos analisar e dar maior atenção a estes dados.
- O segundo gráfico exibe a curva normal reduzida permitindo verificar se a distribuição dos dados tendem a se aproximar da distribuição norma [ 68 , 90 , 95 ].
11. PROJEÇÃO DE VALORES
- O “intervalo de confiança” é utilizado para medir a precisão da avaliação.
- O “campo de arbítrio” deve ser utilizando para tratar singularidades dos imóveis que estão sendo avaliados pela impossibilidade de coletar informações no mercado imobiliário. O campo de arbítrio está limitado a uma semi-amplitude em torno do valor pontual de +- 15%.
- Arredondar o valor final em até 1% do valor adotado é uma sugestão da NBR 14653.
12. FUNDAMENTAÇÃO – O grau final de fundamentação do trabalho pode ser enquadrado em Grau III, II ou I. Caso não seja possível alcançar o Grau I o trabalho não será classificado na fundamentação e os motivos que impediram de obter pelo menos o grau I devem ser explicitados no Laudo de Avaliação.