Categoria:Regressão Linear: mudanças entre as edições

REGRESSÃO LINEAR MÚLTIPLA

Na Avaliação de Bens, os modelos de regressão são construídos com os seguintes objetivos:

1. Predição - Este é o uso mais comum na avaliação de bens. Uma vez que esperamos que grande parte da variação dos preços dos imóveis seja explicada pelas variáveis de entrada (características intrínsecas e extrínsecas), podemos utilizar o modelo para obter valores de Y (valor do Imóvel) correspondentes a valores de X (características) que não estavam entre os dados. Esse procedimento é chamado de predição e, em geral, usamos valores de X que estão dentro do intervalo de variação estudado. A utilização de valores fora desse intervalo recebe o nome de extrapolação e deve ser usada com cuidado especial (conforme a NBR 14653), pois, o modelo adotado pode não ser adequado fora do intervalo estudado. De certa forma, a predição é a aplicação mais comum dos modelos de regressão;

1. 1. Seleção de variáveis - Para estudos de demanda e índices de valorização imobiliária, normalmente as variáveis que afetam significativamente a variação de preços não são exatamente conhecidas (chamadas de cesta básica). Para responder a esse tipo de questão, estudos são realizados com um grande número de variáveis. A análise de regressão pode auxiliar no processo de seleção de variáveis eliminando aquelas cuja contribuição nos resultados não seja importante ou insignificante;

1. 1. 1. Estimação de parâmetros - Em estudos de viabilidade econômica de empreendimentos imobiliários, quando é dado um modelo e um conjunto de dados referente aos preços praticados e os atributos destes imóveis, estimar parâmetros ou ajustar um modelo aos dados significa obter valores ou estimativas para os parâmetros, por algum processo, tendo por base o modelo e os dados observados; A partir desta análise é possível estudar o empreendimento ou mercado local;

1. 1. 1. 1. Inferência - Avaliação pontual ou intervalar? O ajuste de um modelo de regressão em geral tem por objetivos básicos, além de estimar os parâmetros, realizar inferências sobre eles, tais como, testes de hipóteses e intervalos de confiança. A avaliação intervalar foi mais bem definida na revisão da NBR 14653-2, que ocorreu em 2011;

As relações que podem ser descritas por um modelo de regressão linear múltipla são comuns no campo da Engenharia de Avaliações. A formulação mais simples para explicar o comportamento dos preços no mercado imobiliário, pela metodologia tradicional, é representada pela equação (3.1) (Kmenta, 1988).

Onde é a variável dependente ou explicada, são as variáveis independentes ou explicativas, normalmente associadas às características físicas, de localização, e aos aspectos econômicos, são denominados de parâmetros da população e são os erros aleatórios do modelo. A letra minúscula i refere-se à i-ésima observação e a segunda letra minúscula usada identifica a variável independente em questão. A estimação dos parâmetros é feita por inferência estatística com base em uma amostra representativa do segmento de mercado em análise, realizada pelo método dos MQO. O vetor de coeficientes do modelo, também chamado de vetor de preços implícitos ou hedônicos, é obtido por (3.2) (Kmenta 1988).

Constata-se que, da combinação linear dos preços implícitos de cada uma das características do imóvel e as respectivas quantidades demandadas, chega-se ao valor estimado de mercado do imóvel. Para que os parâmetros inferidos no mercado, pelo método dos MQO, sejam não-tendenciosos, eficientes e consistentes , alguns pressupostos sobre as variáveis independentes, os resíduos e a especificação do modelo devem ser atendidos: as variáveis independentes não devem conter nenhuma perturbação aleatória e não deve existir nenhuma relação linear exata ou quase exata entre as mesmas; os erros aleatórios satisfazem as hipóteses de variância constante (modelo homocedástico), normalidade e ausência de autocorrelação; e ainda que o modelo esteja corretamente especificado, ou seja, na sua composição estejam incluídas apenas variáveis explicativas relevantes, e a escala das variáveis qualitativas envolvidas seja adequadamente escolhida, com o objetivo de garantir a linearidade do modelo. Este modelo é denominado de Modelo Clássico de Regressão Linear – MCRL (Gujarati, 2000). Em geral, quando se trabalha com dados de corte transversal não faz sentido testar a autocorrelação dos erros aleatórios, sendo este cuidado indispensável em dados de séries temporais.

1.1 REPRESENTAÇÃO GRÁFICA DA REGRESSÃO LINEAR

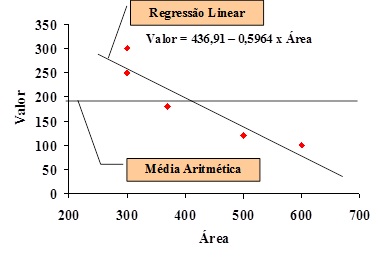
A representação gráfica de um modelo de regressão linear simples é uma reta que está à menor distancia medida na vertical, dos pontos observados, dispostos em um plano formado por dois eixos cartesianos, sendo normalmente utilizado um eixo horizontal para variável independente e o eixo vertical para a variável dependente (FIGURA 3.1).

Quando o modelo é composto por duas variáveis independentes, os pontos estão dispostos no espaço, formado por três eixos cartesianos, sendo um para a variável dependente, e um para cada variável independente. Cada eixo pode ser representado por um vetor. A situação ideal é aquela em que cada vetor seja independente, ou seja, o seu produto escalar é nulo. Uma situação oposta seria aquela onde existe uma dependência linear perfeita entre as variáveis independentes, ocasionando a multicolinearidade entre seus eixos. Desta forma haveria a perda de uma dimensão do espaço, tornando-se impossível a estimação dos parâmetros da regressão. Na prática, ocorre uma situação intermediária entre a multicolinearidade e a ausência total desta, devendo o avaliador investigar até que grau esta interferência entre as variáveis independentes torna-se prejudicial ao modelo.

1.2 HIPÓTESES BÁSICAS

Os modelos de Regressão Linear Múltipla estão sujeitos às hipóteses básicas e que se resumem, de forma geral, na verificação da normalidade, homocedasticidade, não auto-regressão e graus de colinearidade. Em Gonzalez (2003), se relacionam as causas das rupturas destes pressupostos básicos da regressão linear na Engenharia de Avaliações. Normalmente estas causas são devidas à distribuição espacial dos dados que provoca a autocorrelação espacial, ao desconhecimento da forma da linha de regressão, que supostamente pode assumir a forma não linear, à não normalidade dos resíduos e à multicolinearidade, com a influência simultânea de diversos atributos dos imóveis.

Em Kmenta (1978) ressalta-se o fato de que grande parte da econometria moderna deve sua existência à descoberta de que os estimadores dos MQO são, de fato, inconsistentes. Em Costa Neto (2000) ressalta-se que, quando a linha da regressão não é conhecida de antemão, esta deve ser inferida juntamente com os parâmetros da regressão. No caso da regressão linear, as soluções obtidas com o método dos MQO estão restritas aos modelos lineares em seus parâmetros, restringindo o leque das soluções viáveis aos problemas a serem estudados.

As principais dificuldades para a modelagem dos dados utilizando a regressão linear estão ligadas os seguintes fatores:

• A maioria dos modelos apresenta relações não lineares, cujo tratamento não atingiu ainda parâmetros satisfatórios de análise. Neste caso, modelos não lineares podem apresentar melhores resultados. Como artifício matemático é utilizado o procedimento de transformações nas variáveis, buscando linearizá-las;
• As amostras apresentam elevado nível ruído, ou seja, de erros na mensuração das variáveis e no enquadramento correto das características qualitativas dos imóveis;
• O alto grau de colinearidade entre variáveis independentes dificulta a identificação da influência de cada atributo na formação dos preços e consequentemente no valor dos imóveis;
• A dificuldade na definição de escala numérica adequada para estudos de fatores subjetivos ligados às atitudes de compradores e vendedores, expectativas, gosto dos consumidores, disponibilidade de recursos, legislação em curso.
  
  

Conclui-se que existem criticas à adoção exclusiva dos modelos de regressão linear na Engenharia de Avaliações e por estes motivos outras metodologias devem ser testadas.