Categoria:RNA: mudanças entre as edições

REDES NEURAIS ARTIFICIAIS

1.4.1 INTRODUÇÃO

Nesta seção procurou-se descrever com maiores detalhes a parte conceitual, com o objetivo de permitir uma utilização do texto como uma primeira leitura para os profissionais de Engenharia de Avaliações que estejam ingressando nesta área. Os estudos de RNAs são relativamente novos. De 1943, quando da publicação do artigo de autoria de Warren McCulloch e Walter Pitts , até hoje, muitas pesquisas vêm sendo realizadas em todos os âmbitos da ciência, como a medicina, biologia e engenharia. Não existem livros técnicos que tratem com especificidade as RNAs e sua aplicação na Engenharia de Avaliações. Porém, pode-se destacar trabalhos apresentados em congressos dedicados a esta metodologia e voltados para a Engenharia de Avaliações. Alguns colegas de profissão (Guedes 95), que acreditaram e pesquisaram o assunto em exaustão, forneceram subsídios para a aplicação desta metodologia e hoje há como resultado a citação das RNAs como metodologia científica reconhecida na NBR 14653, Avaliação de Bens, Parte 2 – Imóveis Urbanos.

1.4.2 BREVE HISTÓRICO DAS REDES NEURAIS ARTIFICIAIS

As primeiras pesquisas sobre RNAs tiveram início em 1943, com a publicação do artigo “A Logical Calculus of the Ideas Immanent in Nervous Activity”, de autoria de Warren McCulloch e Walter Pitts. Neste artigo, eles estabeleceram as bases da neurocomputação, desenvolvendo procedimentos matemáticos similares ao funcionamento dos neurônios biológicos. Esta contribuição teve um caráter estritamente conceitual, já que os autores não sugeriram aplicações práticas para o seu trabalho, e nem os sistemas propostos por eles tinham a capacidade de aprender. Em 1949, Donald Hebb deu um passo importante na história das RNAs, pois foi o primeiro a propor uma regra de modificação de pesos, criando um modelo de aprendizado. Hebb propôs que a conectividade do cérebro é continuadamente modificada conforme o organismo vai aprendendo tarefas funcionais diferentes e que agrupamentos neurais são criados por tais modificações. Nos anos 50 apareceram implementações de RNAs através de circuitos analógicos e, naquela época, acreditou-se que o caminho para o entendimento da inteligência humana havia sido descoberto. Nathaniel Rochester (1956) desenvolveu uma simulação em computador do neurônio de McCulloch & Pitts, com regra de treinamento Hebbiana. Frank Rosenblatt (1957) desenvolveu o Perceptron, que tinha como objetivo o reconhecimento de padrões ópticos (modelo da visão humana). Em 1958 Rosenblatt introduziu o primeiro modelo de rede neural artificial, estabelecendo a base para a Inteligência Artificial. Bernard Widrow desenvolveu um novo tipo de elemento de processamento de RNAs chamado de Adaline, equipado com uma poderosa lei de aprendizado e que, assim como o Perceptron, ainda possui aplicabilidade na atualidade. Fundou a primeira empresa de circuitos neurais digitais, a Memistor Corporation . Marvin Minsky escreveu o livro Perceptron, onde demonstrava as limitações da Inteligência Artificial. Em uma rigorosa análise matemática ficou comprovado o baixo poder computacional dos modelos neurais utilizados na época, levando as pesquisas neste campo a ficarem relegadas a poucos pesquisadores. Entre a década de 70 e início da década de 80, o período ficou conhecido como a “era perdida no campo de redes neurais artificiais”. Nos anos 80 o interesse pela área retornou, devido, em grande parte, ao surgimento de novos modelos de RNAs, como o proposto por John Hopfield e Teuvo Kohonen . Finalmente em 1986, David Rumelhart desenvolve o algoritmo de backpropagation, ou retropropagação do erro. Foi proposta a sua utilização para a aprendizagem de máquina, e ficou demonstrado como implementar o algoritmo em sistemas computacionais. Além disso, nesta mesma época, ocorreu o surgimento de computadores mais rápidos e poderosos, facilitando a implementação das RNAs. Os engenheiros da computação forneceram os artefatos que tornaram possíveis as aplicações da inteligência artificial.

1.4.3 REDES NEURAIS ARTIFICIAIS NA ENGENHARIA DE AVALIAÇÕES

Por ser recente, esta metodologia ainda é hoje desconhecida pela maioria dos profissionais atuantes na Engenharia de Avaliações. Contudo, alguns pesquisadores já afirmavam a importância deste novo conceito, desenvolvendo pesquisas nesta área, sendo, aliás, responsáveis pelos avanços que culminaram com a aceitação das RNAs como metodologia científica descrita na NBR 14.653 – Avaliação de Bens, Imóveis Urbanos – Parte 2, onde consta no Item 8 - Procedimentos Metodológicos – subitem 8.2.1.4.3 – Tratamento Científico, a seguinte denominação: “Quaisquer que sejam os modelos utilizados para inferir o comportamento do mercado e a formação de valores, devem ter seus pressupostos devidamente explicitados e testados. Quando necessário, devem ser intentadas medidas corretivas, com repercussão dos graus de fundamentação e precisão. Outras ferramentas analíticas, para a indução do comportamento do mercado, consideradas de interesse pelo engenheiro de avaliações, tais como Redes Neurais Artificiais, Regressão Espacial e Análise Envoltória de Dados, podem ser aplicadas, desde que devidamente justificadas do ponto de vista teórico, com inclusão de validação, quando pertinente”. Alguns trabalhos científicos de pesquisadores nesta área, bem como títulos de trabalhos apresentados em congressos e outras reuniões de caráter técnico, podem ser vistos no site da Pelli Sistemas Engenharia Ltda .

1.4.4 CONCEITOS BÁSICOS

As RNAs foram desenvolvidas a partir de uma tentativa de reproduzir em computador um modelo que simule a estrutura e funcionamento do cérebro humano. Uma RNA é um sistema que tem capacidade computacional adquirida por meio de aprendizado e generalização (Braga, Carvalho e Ludemir 2000). O aprendizado está relacionado com a capacidade das RNAs de adaptaram seus parâmetros como conseqüência com a interação com o ambiente externo. A generalização, por sua vez, está associada à capacidade destas redes de fornecerem respostas consistentes para dados não apresentados durante a etapa de treinamento. As RNAs caracterizam-se por possuírem elementos de processamento de estrutura bem simples, inspirados no funcionamento do neurônio biológico, com conexões entre estes elementos de processamento. Cada conexão na rede tem um peso associado e este peso representa a intensidade de interação ou acoplamento entre os elementos de processamento e se a sua natureza é excitatória ou inibitória (Haykin 2001). As RNAs utilizam estruturas neurais artificiais, em que o processamento e o armazenamento das informações são realizados de modo paralelo e distribuído, por elementos processadores de complexidade relativamente simples. Estes elementos podem ser dispostos em camadas responsáveis pelas entradas das informações (camada de entrada – correspondendo às variáveis independentes utilizadas no mercado imobiliário), pelo processamento destas informações (camada intermediária) e pela produção de resultados (camada de saída – que corresponde às variáveis dependentes, normalmente valor unitário ou valor total), para posterior generalização. Um modelo neural biológico consiste em uma rede de células, relativamente autônomas, dotadas, individualmente, de capacidade de processamento limitada. As células são ligadas por conexões, cada uma com um peso associado, que corresponde à influência da célula no processamento do sinal de saída. Pesos positivos correspondem a fatores de reforço do sinal de entrada e pesos negativos correspondem a fatores de inibição (Braga, Carvalho e Ludemir 2000). Os modelos geralmente apresentam um conjunto de células de entrada, por onde são passadas as informações para a rede e um conjunto de células de saída, que apresentam os sinais de saída da rede, e um conjunto de células intermediárias. O conjunto composto pelos neurônios possui uma capacidade bastante poderosa no processamento de informações. Conceitualmente, pode-se considerar que as RNAs são modelos matemáticos que se assemelham à estrutura do cérebro humano e possuem capacidade de aprendizagem para posterior generalização .

1.4.5 O NEURÔNIO NATURAL

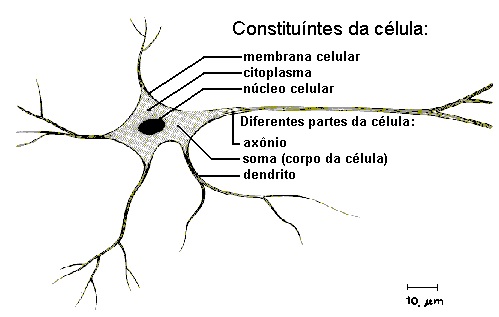
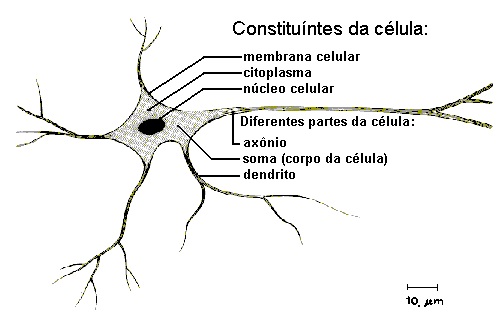
O sistema nervoso humano é responsável pela tomada de decisões e pela adaptação do organismo ao meio ambiente, sendo esta função realizada através de um aprendizado contínuo. Este sistema é constituído de células, responsáveis pelo seu funcionamento, denominadas de neurônios (FIGURA 3.2). O cérebro humano apresenta aproximadamente 10 bilhões de neurônios e cerca de 60 trilhões de conexões entre eles (Haykin, 2001). Estas células recebem, geram e transmitem os estímulos que chegam ou partem do cérebro.

O neurônio é delimitado por uma fina membrana celular que possui determinadas propriedades, essenciais ao funcionamento da célula. A partir do corpo celular projetam-se extensões filamentares, os dendritos, e o axônio (Braga, Carvalho e Ludemir 2000). Os neurônios são definidos como células polarizadas capazes de receber sinais em seus dendritos e transmitir informações por seus axônios. Ao ser excitado, um neurônio transmite informações, através de impulsos, chamados potenciais de ação, para outros neurônios. Estes sinais são propagados como ondas pelo axônio da célula e convertidos para sinais químicos nas sinapses. O neurônio biológico pode ser visto como o dispositivo computacional elementar do sistema nervoso, composto de muitas entradas e saídas. As entradas são formadas através das conexões sinápticas que conectam os dendritos aos axônios de outras células nervosas. Os sinais que chegam por estes axônios são pulsos elétricos conhecidos como impulsos nervosos ou potenciais de ação e constituem a informação que o neurônio processa para produzir como saída um impulso nervoso no seu axônio. Dependendo dos sinais enviados pelos axônios, as sinapses podem ser excitatórias ou inibitórias. Uma conexão excitatória contribui para a formação de um impulso nervoso no axônio de saída, enquanto uma sinapse inibitória age no sentido contrário (Braga, Carvalho e Ludemir 2000). A partir do conhecimento da estrutura e do comportamento dos neurônios naturais foram extraídas suas características fundamentais, utilizadas na criação de modelos de neurônios artificiais que simulam os reais. Estes neurônios artificiais são utilizados na formação das RNAs, se compondo em seus principais elementos de processamento.

1.4.6 O NEURÔNIO ARTIFICIAL – modelo MCP

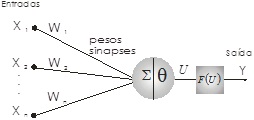
O elemento básico que forma uma RNA é o neurônio artificial (FIGURA 3.3), conhecido também por nó ou elemento processador. Ele foi projetado por McCulloch e Pitts (Haykins 2001) e é baseado no funcionamento de um neurônio natural.

O modelo do neurônio artificial proposto é bem simples. Ele possui n terminais de entrada x1, x2, ..., xn (que representam os dendritos) com pesos acoplados w1, w2, ..., wn a cada entrada, para emular o comportamento das sinapses. Alguns pesos possuem sinais excitatórios (+) e outros sinais inibitórios (-). Os valores de entrada e ativação dos neurônios podem ser discretos, nos conjuntos {0, 1} ou {-1, 0, 1} ou contínuos, normalmente compreendido nos intervalos [0,1] ou [-1,1]. Para cada uma das entradas xi do neurônio da FIGURA 3.3 há um peso correspondente wi. A saída linear u corresponde à soma das entradas xi ponderadas pelos pesos correspondentes wi,dada pela expressão (3.10):

A saída Y do neurônio é obtida pela aplicação de uma função f(u) à saída linear u, indicada por (3.11): 

onde f é chamada de função de ativação e pode assumir diversas formas lineares ou não lineares (Braga, Carvalho e Ludemir 2003).

1.4.7 REDES NEURAIS DE MÚLTIPLAS CAMADAS – MLP

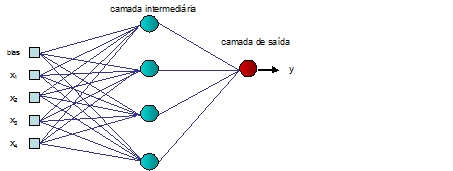
A definição da arquitetura de uma RNA tem sua importância na medida em que restringe o tipo de problema que pode ser tratado. Uma RNA formada por um único elemento processador simples (neurônio artificial), como o apresentado na FIGURA 3.3, está limitada a solução de problemas linearmente separáveis. Existem diversos parâmetros que fazem parte da definição da arquitetura da rede, tais como o número de camadas da rede, número de neurônios em cada camada, tipo de conexão e a topologia da rede (Braga, Carvalho e Ludemir 2000). Uma RNA é, portanto, formada por neurônios artificiais, onde cada neurônio possui capacidade limitada de processamento. Contudo, uma RNA, em função de sua arquitetura e topologia , pode apresentar boa capacidade computacional para a solução de problemas complexos. A FIGURA 3.4 representa uma RNA do tipo feed-forward, na qual cada neurônio executa uma função semelhante àquela da FIGURA 3.3.

A estrutura apresentada possui quatro entradas x1, x2, x3, e x4 e um bias , uma saída y e quatro neurônios na camada intermediária. Esta estrutura é capaz de resolver problemas de regressão, classificação ou predição (Braga, Carvalho e Ludemir 2003). O número de entradas e saídas é em função da dimensão dos dados de entrada e saída, enquanto o número de neurônios nas camadas intermediárias depende da complexidade do problema, exigindo uma quantidade maior de neurônios para problemas mais complexos. Contudo, um número excessivo de neurônios na camada intermediária pode ter como conseqüência a obtenção de resultados indesejáveis, normalmente conhecidos como overfitting . As funções utilizadas para o cálculo de ativação geralmente são não-lineares para garantir a plena funcionalidade das RNAs com múltiplas camadas de neurônios. As funções mais utilizadas são as que possuem um formato sigmoidal, tais como a sigmóide, a tangente hiperbólica, seno, gaussiana, etc.

1.4.8 APRENDIZADO DE REDES NEURAIS ARTIFICIAIS

As RNAs possuem a capacidade de aprender através da apresentação de exemplos. Os dados são apresentados nas entradas para que os parâmetros da RNA sejam ajustados de uma forma continuada, em função do processo de aprendizagem selecionado. Para um determinado conjunto de dados (por exemplo, uma amostra selecionada aleatóriamente no mercado imobiliário), o algoritmo de aprendizado deve ser responsável pela alteração dos parâmetros da rede, para que em um número finito de iterações, hava convergência para uma solução (Braga, Carvalho e Ludemir 2003). O critério de convergência será em função do algoritmo selecionado, existindo diversas implementações destes algoritmos. O objetivo do processo de aprendizado é a convergência para uma solução que será obtida através do ajuste do vetor de pesos w. De forma simplificada, o valor do vetor de pesos w na iteração n + 1 pode ser escrito como na função 3.12,

onde os algoritmos de aprendizado se diferem na maneira de obter o ajuste. Normalmente, estes algoritmos são classificados como aprendizado supervisionado, não supervisionado e aprendizado por reforço. No aprendizado supervisionado existe a presença de um professor ou supervisor, externo à rede, que tem a função de monitorar a resposta obtida para cada vetor de entrada. O conjunto de treinamento é formado por pares de dados de entrada e de saída (características dos imóveis da amostra e os preços coletados), onde se sabe, portanto, qual deve ser a resposta esperada da RNA. O ajuste de pesos é realizado de forma a obter na saída da rede o valor desejado para o imóvel, quando comparado com o preço praticado, dentro dos limites de tolerância inicialmente determinados. As RNAs do tipo MLP utilizam o aprendizado supervisionado. O aprendizado não-supervisionado, como o próprio nome sugere, difere do aprendizado supervisionado, pela inexistência do professor ou supervisor. O aprendizado por reforço pode ser considerado como um meio termo entre os aprendizados supervisionado e não-supervisionado. Maiores detalhes podem ser obtidos em Haykin 2001, Braga, Carvalho e Ludemir 2000, Braga, Carvalho e Ludemir 2003 e Kovács 2002.

1.4.9 DIFICULDADES NO APRENDIZADO E GENERALIZAÇÃO DE REDES MLP

O objetivo principal do processo de aprendizado é obter uma RNA com uma boa capacidade de generalização, tomando como base a amostra ou conjunto de dados coletados no mercado imobiliário. No aprendizado supervisionado, com treinamento por correção de erros, o primeiro algoritmo de treinamento de redes MLP foi descrito em 1986 (Rumelhart, Hinton e Williams) sob a denominação de backpropagation. Este termo se deve ao fato de que o algoritmo se baseia na retropropagação dos erros para realizar os ajustes de pesos das camadas intermediárias (Haykin 2001). Desde então, diversos algoritmos foram propostos, destacando-se o algoritmo Marquardt (Hagan e Menhaj 1994), que apresenta uma eficiência bem superior no treinamento quando comparado com o treinamento com o algoritmo backpropagation. Entretanto, a obtenção de um erro mínimo no processo de aprendizagem não garante a obtenção de valores de mercado consistentes para os imóveis a serem avaliados. Dentre os problemas conhecidos que dificultam a obtenção de uma boa generalização são o overfitting e o underfitting. O overfitting poderá ocorrer quando existir um excesso de neurônios na camada intermediária da rede, ou seja, na situação em que a RNA tem mais pesos do que necessário para a resolução do problema. O underfitting, por sua vez, ocorre quando a RNA possui menos parâmetros do que necessário. Neste caso, devem ser adicionados ao aprendizado, controles sobre o processo de treinamento e generalização, de forma a obter o ajuste ideal (Braga, Carvalho e Ludemir 2003). Existem diversas abordagens para solução destes problemas, entre elas estão os métodos construtivos e os métodos de poda. Os primeiros visam a construção gradual da RNA por meio da adição de neurônios na camada intermediária, até que o ponto ideal entre o treinamento e generalização seja alcançado. O processo se baseia na construção inicial de uma arquitetura com underfitting, e com a adição de neurônios, aproxima-se da arquitetura ideal. Os algoritmos de poda, por sua vez, percorrem o processo inverso, começando com uma estrutura inicial definida de forma empírica, mas visando a diminuição desta estrutura até a obtenção da arquitetura ideal. Os métodos de poda têm sido preferidos em relação aos métodos construtivos, muito em virtude dos algoritmos Optimal Brain Damage – OBD (Cun, Denker e Solla 1989) e Optimal Brain Surgeon – OBS (Hassibi e Stork 1993), descritos de forma resumida na próxima seção.

1.4.10 REDES NEURAIS COM “PODA”

A idéia básica deste método é iniciar a RNA com um número razoável de neurônios na camada intermediária e, durante a etapa de treinamento cortar as conexões (ou pesos) dos neurônios que possuem pouca influência no erro E. Neurônios que tiverem todas as conexões cortadas serão eliminados e, portanto, ao final dos “cortes”, sobrarão somente os neurônios realmente necessários à modelagem. A técnica de poda (Reed, 1993) reduz a complexidade da rede neural, melhorando sua capacidade de previsão, pois evita modelos sobre-parametrizados (muitos neurônios e conexões) em que a possibilidade de sobreajuste (overfitting) é grande. Existem basicamente dois métodos mais utilizados para a poda de RNAs: Optimal Brain Damage (OBD) e Optimal Brain Surgeon (OBS). Em ambos os métodos as conexões (ou pesos) são cortadas e a correspondente variação no erro E, chamada de saliência, é avaliada. No método OBD as conexões são cortadas durante a etapa de treinamento e a RNAs não é retreinada após os cortes. No método OBS, as conexões são cortadas e, após o corte de uma conexão, a RNA é retreinada, permitindo que um número maior de cortes seja efetuado. Além disso, no método OBS a RNA é retreinada, aproximando-se os erros de treinamento por uma função quadrática, de modo a garantir a existência de um mínimo. As técnicas de poda simplificam significativamente o processo de otimização da arquitetura e permite obter modelos com pequena possibilidade de sobreajuste (overfitting). Este fato pode ser observado comparando os resultados obtidos na determinação dos imóveis avaliados utilizando-se RNAs sem poda e com poda conforme será mostrado no próximo capítulo.

1.4.11 POLARIZAÇÃO E VARIÂNCIA

O ajuste da arquitetura das RNAs, com relação ao número de neurônios da camada intermediária, buscando evitar o overfitting ou o underfitting, conforme descrito de forma resumida na seção 3.4.9, tem sido caracterizado como o dilema entre a polarização e a variância (Braga, Carvalho e Ludemir 2003). RNAs com excesso de neurônios na camada intermediária tendem a ter uma maior variabilidade nas respostas (problema da variância), enquanto os modelos com um baixo número de neurônios possuem baixa variância, mas geram respostas polarizadas, ou seja, são direcionadas para determinados resultados (Braga, Carvalho e Ludemir 2003). Essas características das respostas obtidas nas saídas das RNAs são conflitantes, ou seja, a diminuição da polarização poderá levar a uma maior variância, bem como a diminuição da variância pode levar ao aumento da polarização. Para suavização do problema da variância nas saídas das RNAs, foi proposto a aplicação de algoritmos de bagging, que são métodos de geração de múltiplas versões de previsores e a utilização destes em uma árvore de decisão (Breiman 1994). O processo inicia-se pela divisão do conjunto de dados, aleatoriamente, em um conjunto de teste T e um de aprendizagem L, sendo o tamanho de L bem superior ao de T. São construídos então conjuntos de dados LB a partir do conjunto L utilizando-se de técnicas de amostragem. Os conjuntos LB, são utilizados para o treinamento das RNAs. O conjunto de teste T é aplicado ao comitê de RNAs e a média dos resultados destas é comparada ao esperado em T gerando o erro médio quadrático eB. O processo é repetido diversas vezes gerando um erro eB médio. O uso do bagging se torna atrativo quando se deseja projetar uma RNA cujo objetivo seja uma boa generalização (Haykin 2001), que é o caso da construção de RNAs para as avaliações em massa.