Categoria:DEA

Análise Envoltória de Dados - EDO-DEA (VRS)[editar]

O DEA surgiu como instrumento para avaliar a eficiência de um conjunto de unidades de produção, diferindo do enfoque estatístico tradicional na medida em que não se propõe a relacionar uma determinada unidade com a média ou a mediana dos resultados das unidades comparáveis, mas sim com a unidade mais eficiente (benchmarking).

A história começa com a dissertação para obtenção de Ph.D. de Edwardo Rhodes sob a supervisão de W.W. Cooper publicada em 1978. O problema abordado tinha como objetivo desenvolver um método para comparar a eficiência de escolas públicas, sem recorrer ao arbítrio de pesos para cada variável em estudo.

Ao invés de ser um método com enfoque nas medidas de “tendência central”, a intenção é se situar nas unidades extremas que compõem a “fronteira ou envoltória” dos dados. A utilização dessa ferramenta para a engenharia de avaliações foi proposta pela primeira vez por Lyra Novaes, L.F.[2] e pode ser sintetizada da seguinte forma:

• os imóveis que fazem parte da amostra colhida no mercado imobiliário são interpretados no ambiente da metodologia DEA, como as “unidades de produção”;
• para o vendedor do imóvel, os “insumos” (inputs) da sua “unidade de produção” são os atributos (características intrínsecas e extrínsecas) do imóvel relevantes para a sua valorização, como localização, área, etc.; o “produto” (output) da sua “unidade” é o preço, que pode ser expresso pelo Valor Total do Bem;
• para o comprador, inversamente, o input é o preço e os outputs são os atributos (localização, área, etc.);
  
  

Desta forma, ficam constituídas, assim, duas óticas para a DEA:

• a do vendedor e
• a do comprador.
  
  

Para o vendedor, o objetivo é oferecer certos atributos relevantes de um imóvel (área, localização, etc.) e obter por eles o maior preço possível; na visão do comprador, o objetivo é pagar um determinado preço e obter em troca o máximo de atributos relevantes de um imóvel (área, localização, etc.).

Ao coletarmos uma amostra do Mercado Imobiliário, podemos construir, assim, duas fronteiras eficientes: a do vendedor e a do comprador:

• os imóveis que constituem a fronteira eficiente do comprador são aqueles que a partir de atributos relevantes, se paga o menor preço;
• os imóveis que constituem a fronteira eficiente do vendedor são aqueles em que se obtém um máximo de preço, para um dado conjunto de atributos importantes;
• os imóveis compreendidos entre as duas fronteiras (envoltórias de dados) fazem parte do espaço competitivo, sendo possível projetar o seu valor nas duas fronteiras eficientes;
  
  

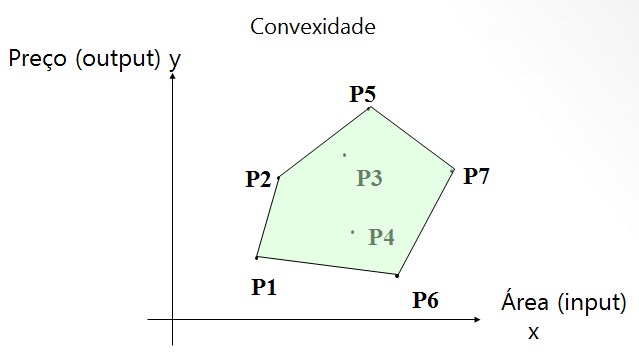
A figura 1 abaixo ilustra uma situação hipotética, onde: Y = preço e X= área, com a definição das fronteiras eficientes para cada uma das duas óticas:

Formulação do Problema - Programação Linear[editar]

O método EDO-DEA para o modelo produto-orientado (no caso da avaliação, corresponde à ótica do vendedor) é a mesma do modelo clássico do DEA e utiliza a mesma formulação do seguinte problema de programação linear:

Problema do Envelope Dual (Ótica do Vendedor)

• Maximizar h, tal que:
  
  

• X_k ≥ λ X
• hY_k ≤ λ Y
• h’ = 1/ h
• λ ≥ 0
• ∑ λ = 1

• Onde:
• h = eficiência
• X = vetor de atributos dos imóveis (insumos)
• Xk = vetor de atributos do imóvel k (insumos)
• Y = vetor de preços dos imóveis (produtos)
• Yk = preço do imóvel k (produto)
• λ = vetor dos pesos da combinação linear dos insumos e dos produtos de unidades eficientes

Na formulação do método EDO-DEA modelo insumo-orientado (ótica do comprador) é feita uma transposição das variáveis do modelo clássico, trocando-se o insumo X pelo produto Y e vice-versa, resultando nas formulações dos seguintes problemas de programação linear:

Problema do Envelope Dual ( Ótica do Comprador )

• Minimizar h , tal que:
  
  
• λ X ≥ X_k
• hY_k ≥ λY
• &lambda ≥ 0
• ∑ λ = 1

• Onde:
• h = eficiência
• X = vetor de atributos dos imóveis (produtos)
• Xk = vetor de atributos do imóvel k (produtos)
• Y = vetor de preços dos imóveis (insumos)
• Yk = preço do imóvel k (insumo)
• λ = vetor dos pesos da combinação linear dos insumos e dos produtos de unidades eficientes

O EDO-DEA permite que cada dado de mercado, com os seus respectivos atributos e preço, possa ser associado a valores nas fronteiras do comprador e do vendedor perfeitamente justificados pelos imóveis eficientes em cada uma das óticas. Torna-se possível, portanto, considerando um conjunto de dados de mercado, estabelecer para um determinado imóvel que se deseja avaliar, que valor ele deveria apresentar para ser considerado “eficiente” do ponto de vista do comprador e que valor ele deveria apresentar para ser “eficiente” do ponto de vista do vendedor, estabelecendo-se um intervalo para a negociação semelhante ao “intervalo de confiança” da inferência estatística.

Aplicação prática – Usando o DEA na Avaliação de Imóveis Urbanos[editar]

Para facilitar o entendimento e comparação de resultados com a Regressão Linear, será apresentado um exemplo do uso do DEA com o software SisDEA Home, utilizando a mesma base de dados utilizada durante o XII COBREAP - CONGRESSO BRASILEIRO DE ENGENHARIA DE AVALIAÇÕES E PERÍCIAS, em BELO HORIZONTE/MG, pelo Engenheiro Sérgio Antão, funcionário da Caixa Econômica Federal.

A partir da base de dados da Tabela 1 abaixo, constituída de 12 apartamentos usados no bairro do Maracanã e de 3 variáveis (preço, área e idade aparente do imóvel), foi realizado o seguinte processo, em 4 etapas, para a aplicação do método DEA e conseqüente identificação dos valores nas fronteiras eficientes de um hipotético apartamento avaliando, com 80 m² de área privativa e 20 anos de idade aparente:

N°	Endereço	Idade	VIDREM	Área (m²)	Preço
		(anos)			(R$ mil)
1	R. Morais e Silva	10	7697	75	105
2	R. S. Francisco Xavier	30	6599	70	50
3	R. Senador Furtado	18	7110	60	90
4	R. Senador Furtado	18	7110	65	95
5	R. Prof. Manoel de Abreu	25	6781	79	80
6	R. Joaquim Palhares	25	6781	65	65
7	R. Jorge Rudge	25	6781	90	75
8	R. S. Francisco Xavier	30	6599	95	100
9	R. Ibituruna	20	7004	72	105
10	R. Morais e Silva	10	7697	90	130
11	R. Morais e Silva	10	7697	90	115
12	R. Morais e Silva	10	7697	90	120

• 1ª Etapa:

Preliminarmente ajustamos as variáveis para a aplicação do método. A variável idade aparente, para ter correlação positiva com a variável preço, foi transformada na variável VIDREM, equivalente a (100* (100 – 10*Ln(Idade))). A variável área manteve-se inalterada. O gráfico de dispersão abaixo ilustra a forma de correlação desta variável independente com a variável dependente:


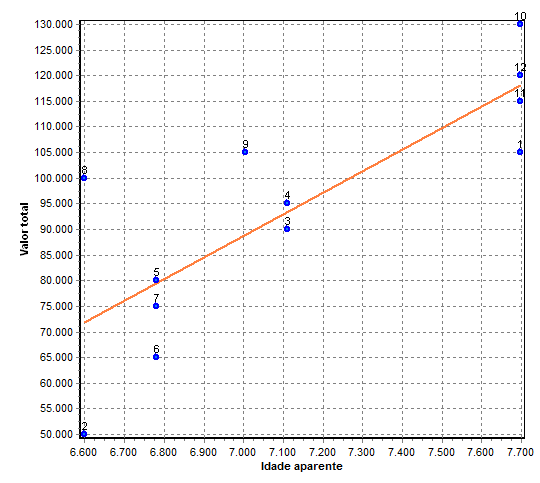
Esta transformação não altera a forma como a variável independente se correlaciona com a variável dependente mas inverte o sentido, que passa a ser positivo.

• 2ª Etapa:

Em seguida, determinamos as eficiências sob cada óptica (modelo VRS) para os 12 apartamentos da base de dados, com a utilização do software SisDEA Home. A partir destes resultados, calculamos os preços máximo e mínimo correspondentes à projeção de cada imóvel nas fronteiras eficientes e calculamos os respectivos IDRF (ver Tabela 2).

Eficiência (VRS)				Preço	Preços nas fronteiras
óptica do vendedor		óptica do comprador		Obs.	Eficientes		IDRF
Unid.	%	Unid.	%	(R$ mil)	Vendedor	Comprador
1	95,89	1	100,00	105.000,00	109.500,47	105.000,00	4,20%
2	100,00	2	100,00	50.000,00	50.000,00	50.000,00	0,00%
3	100,00	3	84,94	89.000,00	89.000,00	75.596,60	16,29%
4	99,25	4	79,58	95.000,00	95.717,88	75.601,00	23,48%
5	87,41	5	82,03	80.000,00	91.522,71	65.624,00	32,96%
6	100,00	6	90,95	65.000,00	65.000,00	59.117,50	9,48%
7	72,27	7	100,00	75.000,00	103.777,50	75.000,00	32,19%
8	100,00	8	100,00	100.000,00	100.000,00	100.000,00	0,00%
9	100,00	9	67,04	105.000,00	105.000,00	70.392,00	39,46%
10	100,00	10	88,46	130.000,00	130.000,00	114.998,00	12,25%
11	88,46	11	100,00	115.000,00	130.002,26	115.000,00	12,25%
12	92,31	12	95,83	120.000,00	129.996,75	114.996,00	12,25%
Tabela 2

• 3ª Etapa:

Introduzimos o apartamento avaliando (com área de 80 m² e idade de 20 anos, ou seja, VIDREM = 7004) no modelo (unidade n° 13), assumindo, como primeira tentativa, um preço próximo à média dos dados de mercado, ou seja, R$ 94 mil. Em seqüência, aplicamos a metodologia descrita na 2ª etapa. Foi observado que a introdução do imóvel avaliando no modelo não foi capaz de alterar as fronteiras eficientes calculadas na 2ª etapa, o que significa dizer que o valor de R$ 94 mil é ineficiente se comparado com os dados de mercado (87,61% de eficiência na óptica do vendedor e 81,08% de eficiência na óptica do comprador). Os valores eficientes seriam respectivamente:

• na óptica do vendedor: R$ 94.000,00 / 0,8761 = R$ 107.293,69
• na óptica do comprador: R$ 94.000,00 x 0,8108 = R$ 76.215,20

• 4ª Etapa:

Esta etapa poderia ser necessária, caso o valor estimado de R$ 94 mil alterasse a estrutura do modelo, modificando qualquer uma das fronteiras. Neste caso, seriam feitas tentativas suplementares, aumentando ou diminuindo o valor inicial de R$ 94 mil, até que não houvesse alteração das fronteiras calculadas para os 12 dados de mercado. Atingido este ponto, procede-se conforme exposto na 3ª etapa.

Como resultado da avaliação, temos um intervalo de valor para o imóvel avaliando compreendido entre R$ 76.215,20 e R$ 107.293,69. Para o apartamento em questão, o comprador poderia perfeitamente justificar o baixo valor com base em certos dados de mercado que contribuíram para conformar a fronteira eficiente sob a sua óptica, assim como o vendedor poderia fazer o mesmo, com base em outros elementos da mesma base de dados.

Comparação dos Resultados com a Regressão Linear[editar]

Realizamos, em seguida, com a mesma base de dados, utilizando DEA e regressão linear múltipla (com as mesmas transformações de variáveis utilizadas no DEA), de forma a poder comparar os resultados estimados para os valores de distintos imóveis avaliandos:

• Imóvel A: 80 m² e 30 anos de idade;
• Imóvel B: 80 m² e 20 anos de idade (mesmo caso utilizado no item 3);
• Imóvel C: 90 m² e 10 anos de idade.

Observa-se que o imóvel A tem atributos inferiores, que o equiparam aos piores do rol de dados de mercado, o imóvel B aproxima-se das condições médias e o C, das condições superiores do mesmo rol. A aplicação dos dois métodos propostos permitiu chegar aos seguintes resultados finais:

Imóvel	DEA			Regressão linear
	óptica comprador	óptica vendedor	IDRF	limite inferior (80%)	limite superior (80%)	IDRF
A	62.502	69.996	11,3%	66.258	83.595	23,1%
B	76.215	107.293	33,9%	85.724	96.374	11,7%
C	115.005	129.993	12,2%	113.173	131.942	15,3%

Tabela 3